Шум ничего не доказывает. Курица, снесши яйцо, часто клохчет так, как будто она снесла небольшую планету.
Марк Твен
Как уже было упомянуто ранее для существования человека в помещении необходимо организовать воздухообмен, наиболее эффективным способом организации является устройство систем приточно-вытяжной вентиляции. Но у подобных систем есть один большой недостаток – шум, который генерируется вентилятором. К шуму вентилятора добавляется аэродинамический шум, который появляется при движении воздуха по воздуховодам.
Прежде чем разбираться с тем, как с шумом бороться и какие именно факторы работы системы вентиляции его порождают и в каком объеме, необходимо разобраться с физикой возникновения и передачи шума.
Если у обывателя спросить про измерение шума, то сразу же получим ответ: децибел. Но что же такое «децибелл»? Давайте разбираться.
Децибел не только не единица измерения звука, он вообще не является единицей измерения, во всяком случае в том смысле, как, например, вольты, метры, граммы и т. д. Одна из измеримых характеристик звука — это количество заключенной в нем энергии, передаваемой посредством механических колебаний воздуха или другой достаточно плотной среды («в космосе ваш крик никто не услышит» (с)). Интенсивность звука (удельную звуковую мощность) в любой точке можно обозначить как поток энергии, приходящейся на единичную площадку, и выразить, например, в ваттах на квадратный метр (Вт/м²), см. рис.1:
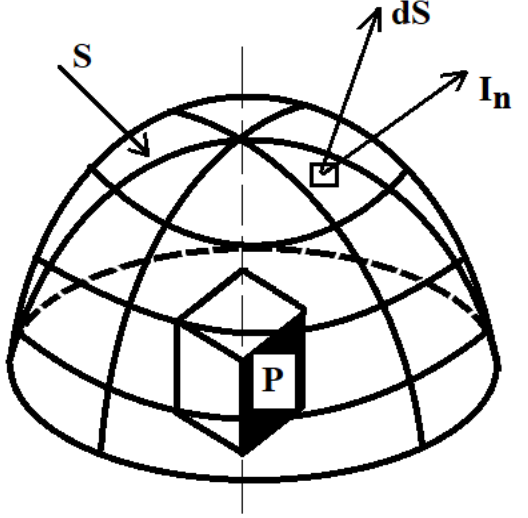
Рис. 1. Иллюстрация звуковой мощности (интенсивности шума)
На рис. 1, источник шума «P», вызывает колебания воздуха, передавая энергию, которая распределяется равномерно по полусфере. Соответственно, чем дальше от источника, тем по большей площади будет распределена генерируемая звуковая мощность, и тем меньше будет интенсивность шума.
При попытке записать в Вт/м² интенсивность обычных шумов сразу же возникают трудности, так как интенсивность наиболее тихого звука, доступного восприятию человека с самым острым слухом, равна приблизительно 0,000 000 000 001 Вт/м². Один из наиболее громких звуков, с которым мы сталкиваемся уже не без риска вредных последствий, — это шум реактивного самолета, пролетающего на расстоянии порядка 50 м. Его интенсивность составляет около 10 Вт/м². А на расстоянии 100 м от места запуска ракеты интенсивность звука заметно превышает 1000 Вт/м². Очевидно, что оперировать числами, выражающими интенсивности звука, лежащие в столь широком диапазоне, очень трудно, независимо от того, представляем ли мы их в единицах энергии или даже в виде отношений. Существует простой, хотя и не вполне очевидный выход из данного затруднения. Интенсивность самого слабого слышимого звука равна 0,000 000 000 001 Вт/м².
Математики предпочтут записать это число таким образом: 10¯¹² Вт/м². Если кому-либо такая запись непривычна, напомним, что 10² это 10 в квадрате, или 100, а 10³ это 10 в кубе, или 1000. Аналогично 10¯² означает 1/10², или 1/100, или 0,01, а 10¯³ это 1/103, или 0,001. Умножить любое число на 10x — значит х раз умножить его на 10 [1].
Пытаясь найти наиболее удобный способ выражения интенсивностей звука, попробуем представить их в виде отношений, приняв за эталонную интенсивность величину 10¯¹² Вт/м². При этом будем отмечать, сколько раз нужно умножить эталонную интенсивность на 10 для того, чтобы получить заданную интенсивность звука. Например, шум реактивного самолета в 10 000 000 000 000 (или в 10¹³) раз превышает наш эталон, то есть этот эталон необходимо 13 раз умножить на 10.
Такой способ выражения позволяет значительно уменьшить значения чисел, выражающих гигантский диапазон звуковых интенсивностей; если мы обозначим однократное увеличение в 10 раз как 1ьбел, то получим «единицу» для выражения отношений. Так, уровень шума реактивного самолета соответствует 13 белам. Бел оказывается слишком большой величиной; удобнее пользоваться более мелкими единицами, десятыми долями бела, которые и называют децибелами. Таким образом, интенсивность шума реактивного двигателя равна 130 децибелам (130 дБ), но во избежание путаницы с каким-либо другим эталоном интенсивности звука следует указать, что 130 дБ определяется относительно эталонного уровня 10¯¹² Вт/м².
Если отношение интенсивности данного звука к эталонной интенсивности выражается каким-нибудь менее круглым числом, например 8300, перевод в децибелы окажется не таким простым. Очевидно, число умножений на 10 будет больше 3 и меньше 4, но для точного определения этого числа необходимы длительные вычисления. Как обойти такое затруднение? Оказывается, весьма просто, поскольку все отношения, выраженные в единицах «десятикратных увеличений», давно вычислены — это логарифмы.
Любое число можно представить как 10 в какой-то степени: 100 это 10² и, следовательно, 2— это логарифм 100 при основании 10; 3 — логарифм 1000 при основании 10 и, что менее очевидно, 3,9191 — логарифм 8300. (Нет необходимости все время повторять «при основании 10», потому что 10 — самое распространенное основание логарифма, и если нет другого указания, то подразумевается именно это основание. В формулах эта величина записывается как lg.)
Пользуясь определением децибела, можем теперь записать уровень интенсивности звука в виде:

Например, при интенсивности звука в 0,26 (2,6×10¯¹) Вт/м² уровень интенсивности в дБ относительно эталона 10¯¹² Вт/м² равен

Но логарифм 2,6 равен 0,415; следовательно, окончательный ответ выглядит так: 10×11,415=114 дБ (с точностью до 1дБ).
Не следует забывать, что децибелы не являются единицами измерения в том смысле слова, как, например, вольты или омы, и что соответственно с ними приходится обращаться иначе. Если две аккумуляторные батареи по 6 В (вольт) соединить последовательно, то разность потенциалов на концах цепи составит 12 В. А что получится, если к шуму в 80 дБ добавить еще шум в 80 дБ? Шум общей интенсивностью в 160 дБ? Никак нет — ведь при удвоении числа его логарифм возрастает на 0,3 (с точностью до двух десятичных знаков). Тогда при удвоении интенсивности звука уровень интенсивности увеличивается на 0,3 бела, то есть на 3 дБ. Это справедливо для любого уровня интенсивности: удвоение интенсивности звука приводит к увеличению уровня интенсивности на 3 дБ.
Интенсивность звука величина, отражающая истинное звуковое восприятие в каждой точки пространства, но в технике, как правило оперируют понятием: звуковое давление. Звуковое давление, также измеряется в дБ и является десятичным логарифмом давления (измеряемого в Па), которое оказывают колебания воздуха, вызванные звуковой волной в конкретной точке пространства:

Где:
– величина звукового давления в точке пространства, Па;
– пороговое звуковое давление (граница восприятия человеческим ухом), ²·¹º¯⁵ Па.
– величина звукового давления в точке пространства, Па;
– пороговое звуковое давление (граница восприятия человеческим ухом), ²·¹º¯⁵ Па.
Применение величины звукового давления для технических расчетов и нормирования [2], связано с тем, что в отличие от интенсивности звука или звуковой мощности, его можно измерить прямым измерением. Принцип измерения уровня звукового давления (УЗД) основан на изменении величины тока или напряжения (выходного электрического сигнала) в электрической цепи постоянного тока, при работе мембраны (мембрана изменяет геометрическую характеристику пространства, тем самым меняя сопротивление цепи, или внося изменения в магнитное поле, косвенно воздействующее на цепь). В зависимости от типа микрофона (шумомера), может быть разный состав электрической цепи (рис. 2 и рис. 3):

Рис. 2. Схема действия динамического микрофона

Рис. 3. Схема действия угольного микрофона
Таким образом в заключении:
1. Звуковая мощность: объективная характеристика источника шума, характеризующее совокупную (полную) энергию звуковой волны, создаваемой источником (осциллятором). Обозначается как Lw;
2. Интенсивность звука: характеристика, отражающая уровень шума в каждой точке пространства;
3. Звуковое давление: характеристика, отражающая уровень шума, измеренный в определенных условиях на заданном расстоянии от источника шума. Обозначается как Lp.
1. Звуковая мощность: объективная характеристика источника шума, характеризующее совокупную (полную) энергию звуковой волны, создаваемой источником (осциллятором). Обозначается как Lw;
2. Интенсивность звука: характеристика, отражающая уровень шума в каждой точке пространства;
3. Звуковое давление: характеристика, отражающая уровень шума, измеренный в определенных условиях на заданном расстоянии от источника шума. Обозначается как Lp.
ВАЖНО:
- нельзя сравнивать величины Lw и Lp. При сравнении источников шума корректнее всего сравнивать уровни звуковой мощности Lw, так как эта величина объективна и не зависит от условий работы источника шума (вент. установки);
-при сравнении источников шума по звуковому давлению (Lp), необходимо удостоверится, что звуковое давление было измерено в одинаковых условиях (по одному нормативу, на одинаковом расстоянии).
Недобросовестные поставщики оборудования часто манипулируют этими величинами, чтобы ввести пользователя в заблуждение.
В следующих статьях мы поговорим о восприятии шума на разных частотах, разберемся, что такое частота шума и какие элементы системы вентиляции наиболее шумные и как с этим шумом бороться.
- нельзя сравнивать величины Lw и Lp. При сравнении источников шума корректнее всего сравнивать уровни звуковой мощности Lw, так как эта величина объективна и не зависит от условий работы источника шума (вент. установки);
-при сравнении источников шума по звуковому давлению (Lp), необходимо удостоверится, что звуковое давление было измерено в одинаковых условиях (по одному нормативу, на одинаковом расстоянии).
Недобросовестные поставщики оборудования часто манипулируют этими величинами, чтобы ввести пользователя в заблуждение.
В следующих статьях мы поговорим о восприятии шума на разных частотах, разберемся, что такое частота шума и какие элементы системы вентиляции наиболее шумные и как с этим шумом бороться.
Статья подготовлена НИИ «ЭТМ» при консультации специалистов НИУ «МЭИ»
Литература
- Р. Тейлор. Шум. М.: Мир, 1978.
- СП 51.13330.2011 «Защита от шума»
